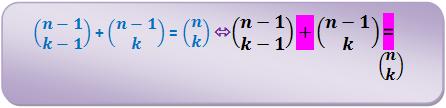Reta final!

Em um piscar de olhos o semestre já está chegando ao fim, já estamos revisando a matéria relembrando os últimos conceitos para ficarmos 100% preparados para prova.

Nesta aula o professor passou um resumo para prova, e tirou algumas dúvidas que estava no ar!

Bom agora o que nos resta é revisar a matéria dada, ler e reler o blog para fazermos a prova tranquilamente!

Beijoooos Juliana!

Dicas!

Booa noite!

Segue um vídeo explicativo com algumas dicas sobre medias, moda, mediana, variância e desvio Padrão.

Variância e Desvio Padrão

Continuando o tema do ultimo post, agora nossa foco será VARIÂNCIA E DESVIO PADRÃO. 

A Variância e o Desvio Padrão são consideradas medidas de dispersão e utilizadas nas situações em que grupos com médias de valores iguais, possuem características diferentes. A Variância estabelece os desvios em relação à média aritmética e o Desvio Padrão analisa a regularidade dos valores. Vamos através de um exemplo prático, demonstrar uma aplicação básica envolvendo as duas medidas. 

Na preparação para os jogos Olímpicos de Atenas, três atletas do salto em altura ao realizarem um treinamento diário, consideraram seus quatro melhores saltos em centímetros. Veja:  

Dentre os atletas, a melhor média foi a do Atleta Z, veja: 

Atleta X = (144 + 171 + 150 + 138) / 4 = 150,75 
Atleta Y = (146 + 170 + 152 + 137) / 4 = 151,25 
Atleta Z = (145 + 169 + 154 + 140) / 4 = 152 
Atleta W = (150 + 167 + 149 + 141) / 4 = 151,75 
Em situações que envolvam disputas olímpicas, o atleta com melhor média, às vezes não é considerado o mais indicado, pois verifica-se a questão da regularidade dos resultados obtidos. É referente a esses casos que aplicamos os cálculos ligados à Variância e ao Desvio Padrão. 

Lembre-se de que o desvio padrão consiste na raiz quadrada da variância. 

Cálculo da Variância e do Desvio Padrão

Atleta X

Atleta Y

Atleta Z

Atleta W

O atleta que obteve o menor Desvio Padrão deve ser considerado o de melhor regularidade em resultados. Dessa forma, temos que o atleta W se enquadra nessa condição de melhor regularidade. 

Segue um vídeo com um exemplo explicativo!

Espero que tenha ficado claro, em breve postaremos algumas dicas para facilitar a resolução de alguns exercícios! Uma ótima semana a todos. Juliana Fernandes.

Desvio Médio Simples

Nesta aula o professor entro no conceito de como calcular o desvio Padrão. Para isso temos que ter claro em nossa mentes o desvio médio simples, assim, ficará muito fácil calcular a variância e o desvio médio padrão, que será nosso próximo post do blog cabeças pensantes! 

Mas enquanto isso vamos deixar claro o que é um Desvio Médio simples.

 O Desvio Médio simples é um medida da dispersão dos dados em relação á média de uma sequência, o “afastamento” em relação a essa média. Esta Medida representa a média das distâncias entre cada elemento amostra e seu valor médio.

Exemplo:

Qual o desvio médio da série ( 3,4,5,6,7) ?

1) Deve-se fazer a média dos números fornecidos 3,4,5,6 e 7 . Essa média é obtida pela soma de todos os valores dividido pela quantidade de valores. No caso: 

Média = (3+4+5+6+7)/5 = 5 

2) Com a média dos valores em mãos, calcula-se o desvio médio, que é a subtração do valor dado pela média dos valores. No caso: 

Dm = 3 - 5 = -2 
Dm = 4 - 5 = -1 
Dm = 5 - 5 = 0 
Dm = 6 - 5 = 1 
Dm = 7 - 5 = 2 

Agora fica fácil..... é só somar tudo em módulo, ou seja, somar tudo como se fossem números negativos: 

Dm = 2 + 1 + 0 + 1 + 2 = 6 !

Espero que tenha ficado claro esse breve resumo de como calcular o Desvio Médio Padrão! Beijos, e até a próxima!

Juliana Fernandes Silva

Triângulo Pascal

Definição :

O Triângulo de Pascal também é conhecido como Triângulo de Tartaglia, trata-se de uma tabela triangular formada por números binomiais de Newton, onde n representa a linha vertical e k representa as colunas horizontais. Os números ficam dispostos de forma que os binomiais de mesmo numerador situam-se na mesma linha e os de mesmo denominador na mesma coluna. 

 Construção do triângulo: 

Para construir um triângulo, basta calcular os números  pela definição. 

Vejamos como construir o triângulo sem calcular cada um dos binomiais. 

a) O primeiro e o último elemento de cada linha são sempre iguais a 1, pois 

b) Os demais elementos de cada linha são obtidos usando a Relação de Stifel. 

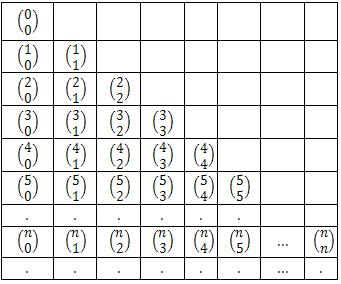
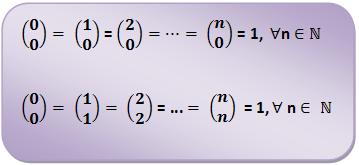
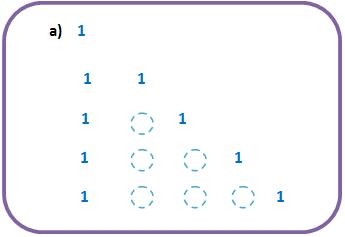
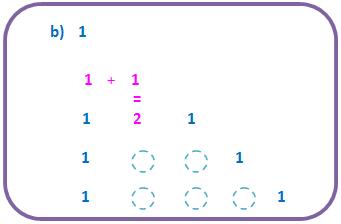
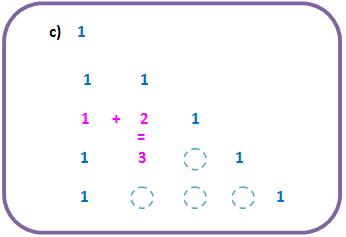
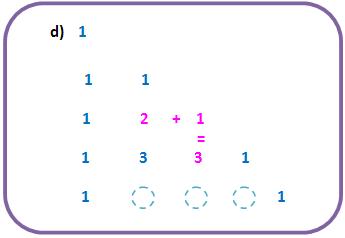
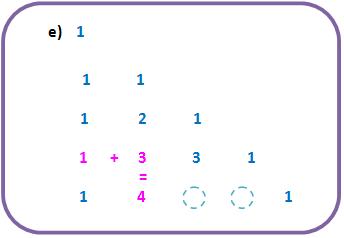
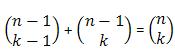Veja estes binomiais de relação  , organizados no Triângulo de Pascal sugerem que a soma de um binomial com o binomial da direita é igual ao binomial abaixo deste último.

E, portanto: 

Dessa forma é possível construir o triangulo:

 Segue um vídeo sobre as curiosidades do triângulo Pascal : 

Bibliografia para aprofundamento :

http://matematicario.blogspot.com.br/2013/06/curiosidades-do-triangulo-de-pascal.html

http://www.colegioweb.com.br/trabalhos-escolares/matematica/binomio-de-newton/triangulo-de-pascal.html

http://www.mat.ufrgs.br/~portosil/histo2b.html

Juliana Fernandes Silva

Teorema Central do Limite

     Em linguagem corretamente simplificada, o teorema central do limite, ou teorema do limite central, em teoria das probabilidades, expressa o fato de que a soma de muitas variáveis aleatórias independentes e com a mesma distribuição de probabilidade tender à distribuição normal, também conhecida como distribuição de Gaussiana.

     Por exemplo, o resultado de um jogar de dados não viciados tem distribuição de probabilidade retangular, isto é, todos os resultados possíveis têm a probabilidade de 1/6. Já a distribuição de probabilidade da soma dos valores obtidos num jogar de vários dados tende a forma gaussiana.

     Como grande parte das características naturais são resultados de diversos fatores, com grande freqüência nos deparamos com a distribuição normal .

  

Vídeo explicativo: 

http://www.youtube.com/watch?v=zEwT_fIpSBE

Juliana Fernandes Silva

Pirâmide do conhecimento

Muitas pessoas jogam diversos jogos que utilizam dados, porém não sabem o motivo pelo qual esses dados possuem de 1 a 6 “furinhos” distintos em cada face da sua forma cúbica, para aqueles que não perceberam a soma dos opostos do cubo deve ser 7!

Bom, hoje o professor Valente resolveu usar um pouco de “Mágica” em nossa aula  usando os dados para explicar melhor sobre estatística e fez até uma dinâmica.

Com uma caixa cilíndrica com as tampas ovulada, ele inseriu dois dados dentro e ao dar duas batidas “adivinhava” os resultado dos dados, puro truque rs, como a caixinha é ovulada os dados não conseguem passar pelo centro assim giram pelas bordas (90º graus) ao bater duas vezes a caixinha os dados viram 108º graus como sabemos que a soma dos opostos é sempre 7, basta guarda mentalmente os números originais! 

Tudo isso para entendermos melhor sobre  a pirâmide do conhecimento ela estruturada em quatro divisão, os dados, informações, conhecimentos e por fim a sabedoria. 

Os dados e informação fazem parte dos dados mais estruturados, e podem ser incluídos em grandes bancos de dados o que tornam a consulta e utilização menos descomplicada. Os dados são o menor valor da informação, que é o conjunto dos dados.

O Conhecimento é a conversão das informação em algo mais permanente, podendo recorrer a ela a qualquer momento. A Sabedoria é a evolução do conhecimento, a cada momento sofremos influência sob o meio de experiências que vivemos e/ou sentimos, e agimos de forma adequada, confirmando ou não o conhecimento.

Bom, este foi um pequeno resumo do que aprendemos na a aula , esperam que tenham gostado, e até semana que vem! 

Juliana Fernandes Silva